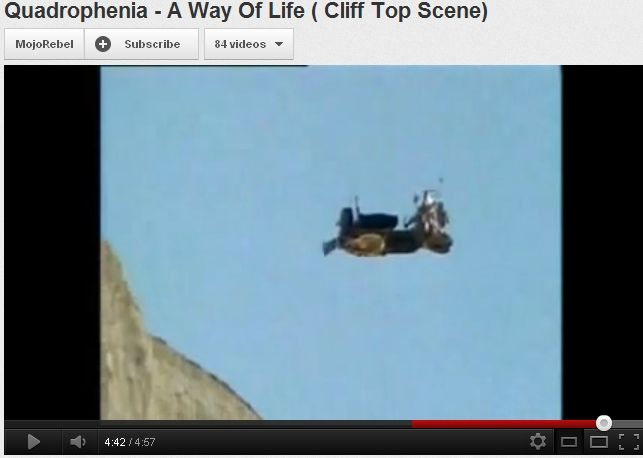
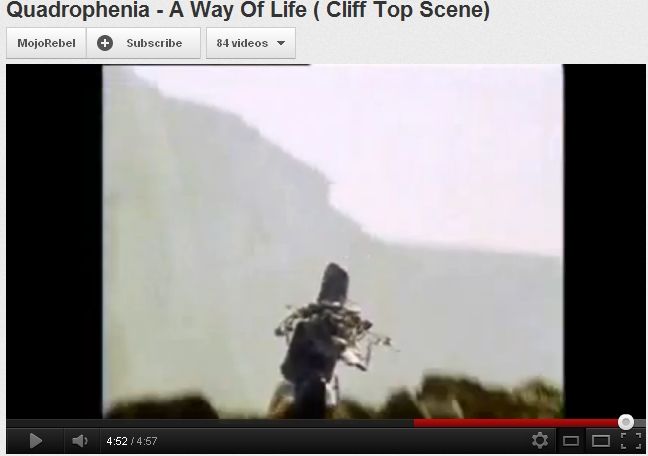
/\ we need to know
(a) the terminal velocity for a BX
(b) the time it takes to reach that terminal velocity
(c) the distance travelled to reach that terminal velocty
(d) then we can work out the remaining distance to travel at that terminal velocity, and hence the time over that remaining distance
(e) the total time taken will be time from (b) plus time from (d)
For this, we need to use
Newton's 3 equations of motion
1a) v= u + at
1b) s = ut + ½at²
1c) v² = u² + 2as
Newton's 2nd law of motion
2) F=ma
and the force acting on a body due to aerodynamic drag
3) F = ½ ? C A v²
[ .... in the above equations
? is the air density (1.293 at STP)
C is the drag co-efficient of the body (say 0.34 for a BX falling nose first)
A is the cross-sectional area of the body (say 2.4 m² for a BX falling nose first)
m is the mass of the body (say 1000 kg for a BX)
v is the terminal velocity of the body in m/s
u is the initial velocity of the body in m/s (say 0)
t is time over the interval in question in secs
s is the distance over the interval in question in metres
a is acceleration due to gravity (9.811 m/s²) ..... ]
At terminal velocity, equations (2) and (3) are balanced
so ma = ½ ? C A v²
i.e. v² = ma ÷ (½ ? C A) = 1000 x 9.81 ÷ (½ 1.293 x 0.34 x 2.4) = 9811 ÷ (0.527544) = 18597.5
answer (a) v = 136 m/s (306 mph)
although the acceleration due to gravity will reduce as the drag builds up, to keep is simple we can use equations 1a and 1c to calculate the time and distance to reach the terminal velocity
answer (b) t = (v-u) ÷ a = 136 ÷ 9.811 = 13.86 secs
answer (c) s = v² ÷ 2a = 18597.5 ÷ (2 x 9.811) = 948 metres
To get the remaining distance, 1 mile = 1609 metres, it has fallen 948 metres, so there are 661 metres to fall at 136 m/s
answer (d) remaining time = 661 ÷ 136 = 4.86 secs
answer (e) the total time for a BX to fall nose first from 1 mile up = 13.86 + 4.86 =
18.72 seconds ...... and it
hits the ground at 306 mph ... these answers assume we fit streamers from the rear wing to stop it tumbling
In top gear they estimated that the Beetle would take between 36 to 40 secs to fall 1 mile
 The reason it takes 36 to 40 secs is that they dropped it with wheels facing downwards
The reason it takes 36 to 40 secs is that they dropped it with wheels facing downwards
 and Richard Hammond says that it reaches a terminal velocity of 125 mph (but it tumbles as it drops)
and Richard Hammond says that it reaches a terminal velocity of 125 mph (but it tumbles as it drops)
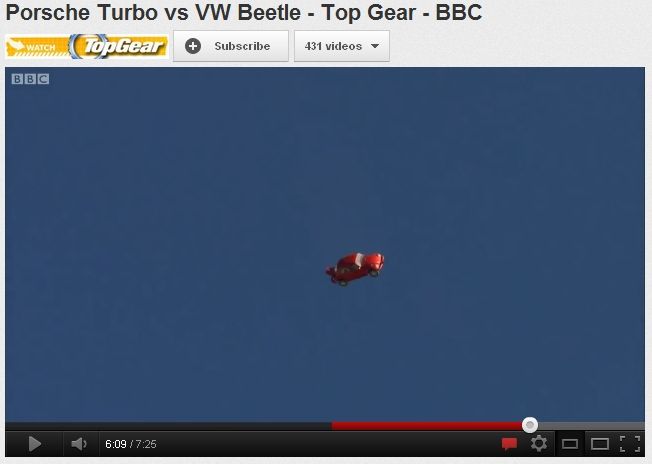
The easiest way to estimate a car dropping in that way, is to take A as the cross-sectional area of the underside, and use a vale for C of about 2.1 (a square box)
I'll let someone else do that, just repeat what I did, but use the new values (I now wish I'd done it in a spreadsheet rather than on the back of an envelope, and I can't be arsed to copy my typing with new numbers).
For a scooter going off Beachy head (160 metres high)
.... we only require equations 1b and 1a because I doubt if it reaches terminal velocity (assuming again a constant acceleration, to keep it simple)
[ also, it's difficult to work out whether ithe scooter would reach terminal velocity, because the co-efficient of drag for a tumbling scooter could continually vary between 0.6 (nose down) and 1.4 (similar to horizontal skydiver), with varying cross-section. Maybe try it wheels down with C of 1.4 and measure the underside of a scooter for cross-section, then do (a), (b), (c) to see if it reaches terminal veocity in less than 160 metres. But I reckon it hits the ground before reaching terminal velocity ]
Using equation 1b
s = ut + ½at²
u is the initial vertical velocity, which is zero. s is the height, which is 160.
so 160 = 0 + ½ 9.811 x t²
i.e. t² = 32.616, so t = 5.711 secs
using equation 1a
v = u + at = 0 + 9.811 x 5.711 = 56 m/s = 126 mph
The horizontal distance depends on the horizontal speed just before it leaves the top. Say 60mph i.e. 100 kph i.e. 27 m/s.
It falls for 5.711 secs, and to keep it simple assume the drag doesn't reduce its horizontal speed in that time.
So horizontal distance travelled = 27 x 5.711 = 154 metres
i.e. it keeps travelling horzontally at 60 mph, while it accelerates vertically from 0 to 126 mph, hitting the ground 5.711 seconds later, having fallen 160 metres and travelled 154 metres from the cliff bottom (assuming a vertical cliff).
In 'Quadrophenia', it looked to me as if they secured the handlebar stem to limit the steering, set the throttle at say half way, then someone stood at the side and pulled the clutch lever, moved it to say 1st gear then let the clutch out as they ran alongside and then left it to go over the cliff. They would have decided where they wanted it to hit the ground so the cameraman would be in the right place, then knowing the horizontal distance from cliff bottom and the time it takes to fall, you work out the horizontal speed you want it to leave the top of the cliff (10 mph would be ~25 metres)